Answer The domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same yvalueI'll be breaking down this question in three parts, 1 When x is positive 2 When x is negative 3 When x is zero In the first case, if x is positive, And since the modulus of a positive number is the number itself, our function becomes, f(x) = x/ Given f(x) = √x 1 To find the domain and range of function Explanation So the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f(x) = √x 1 Now for real value of x1≥0 ⇒ x≥1 Hence the domain of f = 1, ∞) And the range of a function consists of all the second
Http Fsw01 c Cuny Edu Luis Fernandez01 Web Teaching Classes Math30 Nikos 30sp10 Funex Pdf
F(x)=x+1 domain and range
F(x)=x+1 domain and range-We can see the function a define for all values of x Domain of f(x) = R, where R is the set of all real number When you put any value of x from domain you'll get either '0′ or any positive value for f(x) So, Range of f(x) = 0, ∞) Graphical Method Simply draw the graph and you can see domain & range in graph itself 1 f(x)= x 1 Find the domain, range, and intercepts of the function Then find the minimum and maximum values on the interval 0, 3
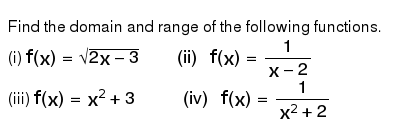



Find The Domain And Range Of The Following Functions I F X Sqrt 2x 3 Ii F X 1 X 2 Iii F X X 2 3 Iv F X 1 X 2 2
Rational functions f(x) = 1/x have a domain of x ≠ 0 and a range of x ≠ 0 If you have a more complicated form, like f(x) = 1 / (x – 5), you can find the domain and range with the inverse function or a graph See Rational functions Sine functions and cosine functions have a domain of all real numbers and a range of 1 ≤ y ≤ 1Domain and Range of Exponential and Logarithmic Functions Recall that the domain of a function is the set of input or x values for which the function is defined, while the range is the set of all the output or y values that the function takes A simple exponential function like f(x) = 2x has as its domain the whole real lineHow to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support
Range {yly>0} domain {x\x> 1/6); f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞) And the range of a function consists of all the second elements of all the ordered pairs, ie, f(x), so we have to find the values of f(x) to get the required range Now we know for this function x5>0 taking square root on both Find the domain and range of the real function f (x) = x/1x^2 ━━━━━━━━━━━━━━━━━━━━━━━━━ ️Given real function is f (x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R
What is the domain and range of this function?Function should remain real so math√(x^2–1)/mathshould not be equal to zero so math x^2–1 \neq 0/math mathx^2=1/math Or mathx=\pm 1/math AndRead the book Dr Pan just finished!!Grab a copy here h



Domain And Range Of Rational Functions



Domain And Range And Composition Of Functions
Find the domain and range of the function `f (x)= (1)/sqrt (x5)` Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device UpCalculus Find the Domain and Range f (x)=1/ (x7) f (x) = 1 x − 7 f ( x) = 1 x 7 Set the denominator in 1 x−7 1 x 7 equal to 0 0 to find where the expression is undefined x−7 = 0 x 7 = 0 Add 7 7 to both sides of the equation x = 7 x = 7 The domain is all values of x x that make the expression defined Interval NotationNEW Interested in Finding Out the Top "{{3}} Challenges that Can Get YOU in Trouble with Math"?




Let F X Ln X Y 1 Find And Sketch The Domain Of F What Is The Range Of F Study Com




Find The Domain And Range Of The Function F X Chegg Com
Range {yly> 2} domain {x x g According to the United States Postal Service, First Class Mail International (letters) takes 6 to days to deliver to their destination In order to test this, Greg, in Chicago, sent oneThe domain and range are the intervals in which the function is defined in the x and y axes Answer and Explanation 1 Become a Studycom member to unlock this answer! 2x 1 = 0 2x = 1 x = 1 / 2 Therefore , Domain = R { 1/2 } All real numbers are used as range here For getting solve the denominator of the given fraction and reduce the value of x from the real number "R" Hope it helps you dude



Solution Sketch F X X 1 If X Lt 1 0 If 1 Amp 04 X Amp 04 1 X 1 If X Gt 1 Find The Domain And Range Using Interval Notation




Find Domain And Range Of F X X 1 C 2x 8 Maths Relations And Functions Meritnation Com
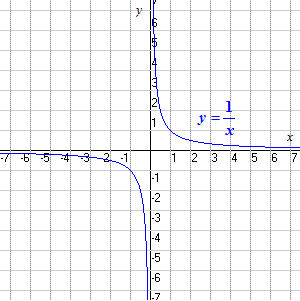
What are the domain and range of f (x) = (1/6)^x 2?To find the domain, let f(x)=1/log(2x) is not defined for 1 2xWhat is the domain and range of f (x) = 1/x?



3 3 Domain And Range Mathematics Libretexts




Find The Domain And Range Of The Function F X 2 X 5
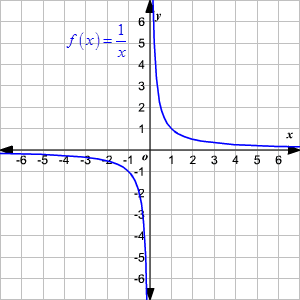
Given f(x) = 1/𝑥 , x ∈ R – {0} Finding f(x) at different values of x f(−2) = 1/(−2) = – 05 f(−15) = 1/(−15) = −10/15 = −2/3 = – 066 f(−1) = 1/(−1) = −1 f(−05) = 1/(−05) = −10/5 = – 2 f(025) = 1/025 = 100/25 = 4 f(05) = 1/05 = 10/5 = 2 f(1) = 1/1 = 1 fThe "" means "such that," the symbol ∈ means "element of," and "ℝ" means "all real numbers" Putting it all together, this statement can be read as "the domain is the set of all x such that x is an element of all real numbers" The range of f (x) = x2 in set notation is R {y y ≥ 0} R indicates rangeFind Domain and Range of real functions (1) `f(x)=(x2)/(3x)` (2)`f(x)=1/sqrt(x5)` (3) `f(x)=x/(1x^2)`



3
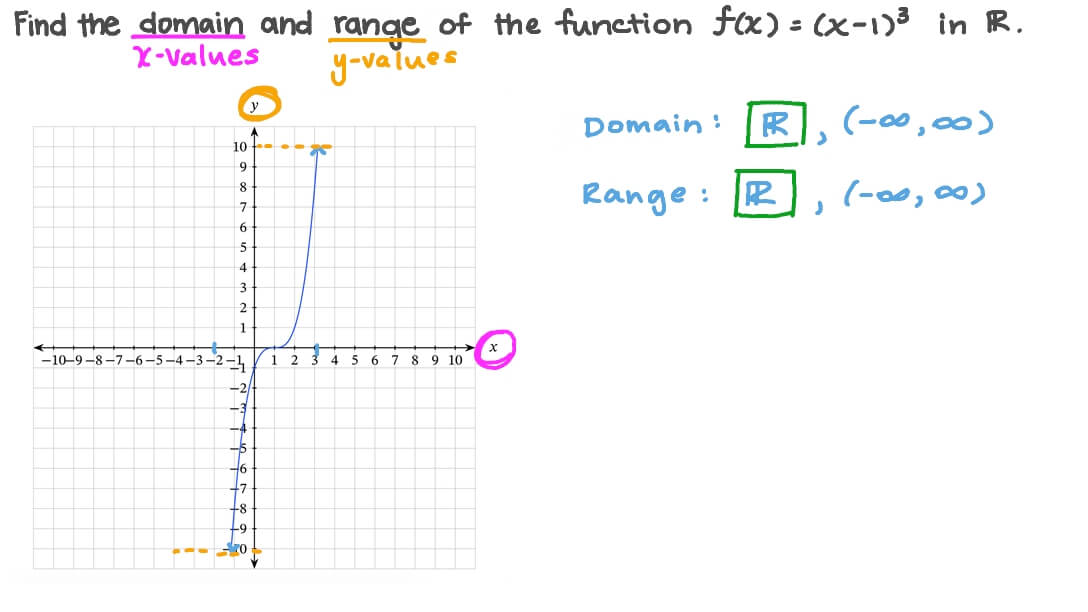



Question Video Finding The Domain And Range Of A Cubic Function Given Its Graph Nagwa
114 Range of a function For a function f X → Y the range of f is the set of yvalues such that y = f(x) for some x in X This corresponds to the set of yvalues when we describe a function as a set of ordered pairs (x,y) The function y = √ x has range;Question 1 Find the domain and range of the following functions f(x) = x 3 Solution Domain A set of all defined values of x is known as domain Range The out comes or values that we get for y is known as range Domain for given function f(x) = x 3 For any real values of x, f(x) will give defined values Hence the domain is RThe Domain and Range of a Function The domain of a function is the set of values for the variable in which the function is defined or real On the




Interpretation Of Domain And Range Of A Function F Ppt Download
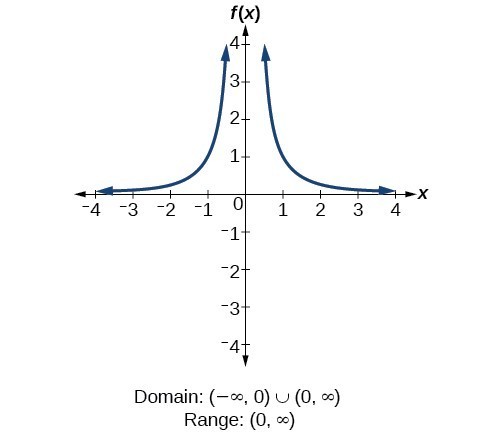



Find Domains And Ranges Of The Toolkit Functions College Algebra
The terms within the radical are x 3 Find domain and range of f (x)= square root of (x 1) (3 x) Enter your answer for the domain using interval notation Set the radicand in greater than or equal to to find where the expression is defined Fx x 2 2 x 1 Solution to Example 3 Explanation h(x) = 1 x 1 Domain Denominator must not be 0 ∴ x 1 ≠ 0 or x ≠ − 1 Domain is any real value except −1 So Domain is R,x ≠ − 1 Range is any real value except 0 So Rage is R,h(x) ≠ 0 graph {1/ (x1) 10, 10, 5, 5} Ans Answer linkFind the Domain and Range f (x)=1 f (x) = 1 f ( x) = 1 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x



Introduction To Domain And Range Relations And Functions Geeksforgeeks



Domain And Range Of Rational Functions
Find the domain and range of the function f (x) = 2 − sin3x1 Solution Solution f (x) = 2 − sin3x1 Here, 2 − sin3x can never be zero as sin3x will always less than 2 ∴ Domain of f (x) will be x ∈ R Now, f (x) will be maximum when 2 − sin3x is minimum 2 − sin3x will be minimum when sin3x = 1Algebra Find the Domain and Range f (x)=1/ (x1) f (x) = 1 x − 1 f ( x) = 1 x 1 Set the denominator in 1 x−1 1 x 1 equal to 0 0 to find where the expression is undefined x−1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1 For example, the function \(f(x)=\dfrac{1}{\sqrt{x}}\) has the set of all positive real numbers as its domain but the set of all negative real numbers as its range As a more extreme example, a function's inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an



Www Math Colostate Edu Clayton Teaching M113f09 Homework Hw1solutions Pdf




The Problem Was To Graph The Function Find The Chegg Com
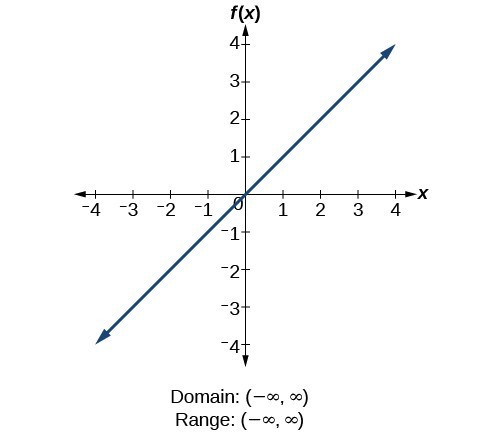
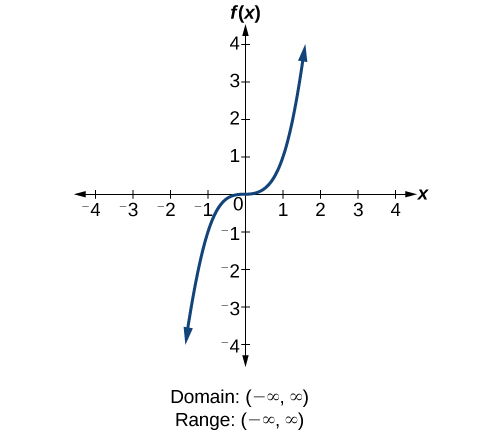
Find the Domain and Range f (x)= (x1)/ (x1) f (x) = x − 1 x 1 f ( x) = x 1 x 1 Set the denominator in x−1 x1 x 1 x 1 equal to 0 0 to find where the expression is undefined x1 = 0 x 1 = 0 Subtract 1 1 from both sides of the equation x = −1 x = 1To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find domain and range of `f(x)=x/(1x^2)`For example, a function f (x) f ( x) that is defined for real values x x in R R has domain R R, and is sometimes said to be "a function over the reals" The set of values to which D D is sent by the function is called the range Informally, if a function is defined on some set, then we call that set the domain



What Is The Domain And Range For The Following Function And Its Inverse F X 3x 1 2 Mathskey Com




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot
All real y ≥ 0 Example a State the domain and range of y = √ x4 b SketchFigure 3 Domain and range of a function and its inverse When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function For example, the inverse of f ( x) = x \displaystyle f\left (x\right)=\sqrt {x} f (xArithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution f(x)=\frac{1}{x^2} domain\y=\frac{x}{x^26x8} domain\f(x)=\sqrt{x3} domain\f(x)=\cos(2x5) domain\f(x



Solution Find The Domain An Range Of F X X 1 X
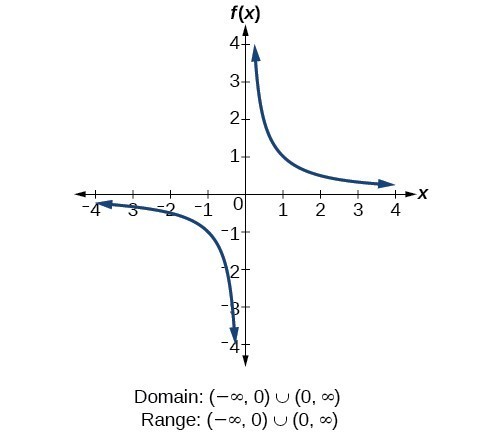



Find Domains And Ranges Of The Toolkit Functions College Algebra
Transcript Misc 5 Find the domain and the range of the real function f defined by f (x) = x – 1 Here we are given a real function Hence, both domain and range should be real numbers Here, x can be any real number Here, f (x) will always be positive or zero Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that range f (x) is 0 or positive numbers, So range cannot be negative Hence, RangeFind the Domain and Range f (x)=1/x f (x) = 1 x f ( x) = 1 x Set the denominator in 1 x 1 x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x that make the expression defined Interval Notation Misc 4 Find the domain and the range of the real function f defined by f(x) = √((𝑥−1)) It is given that the function is a real function Hence, both its domain and range should be real numbers x can be a number greater 1 Here, f(x) is always positive, Minimum value of f(x) is 0,




Find Domain And Range F X X 1 X 1 Maths Relations And Functions Meritnation Com




Find Domain And Range Of Function Y 1 X 2 Youtube
Solution We have, f(x) = 1 1 − x2 Clearly, f(x) is defined for all x ∈ R except for which x2 − 1 = 0 ie, x = ± 1 Hence, Domain of f = R − { − 1, 1} Let f(x) = y Then, 1 1 − x2 = y ⇒ 1 − x2 = 1 y ⇒ x2 = 1 − 1 y = y − 1 yThe given real function is f (x) = x − 1 It can be seen that x − 1 is defined for (x − 1) ≥ 0 ie, f (x) = (x − 1) is defined for x ≥ 1 Therefore the domain of f is the set of all real numbers greater than or equal to 1 ie, the domain of f = 1, ∞) For instance, f(x) = itex\frac{1}{x3}/itex The domain is simply the denominator set equal to 0, {xl x≠3} However, range is found by solving for (isolating x to one side) and setting the denominator equal to zero x = itex3\frac{1}{y}/itex So range is {xl x≠0} This is a systematic method that I assume is the only way to find the range



What Is The Domain And Range Of 1 X 3 Quora



Http Fsw01 c Cuny Edu Luis Fernandez01 Web Teaching Classes Math30 Nikos 30sp10 Funex Pdf
All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f (x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f (x) = √ ( (9 −x^2)) It is given that the function is a real function




Answered 6 Determine The Domain And Range Of Bartleby




Find The Domain And The Range Of The Real Function Defined By F X Sqrt X 1



3




Domain Range F 1 All X Such That F X 1 X Chegg Com



Search Q Domain And Range Table Tbm Isch



Answer In Algebra For Dani Wagas
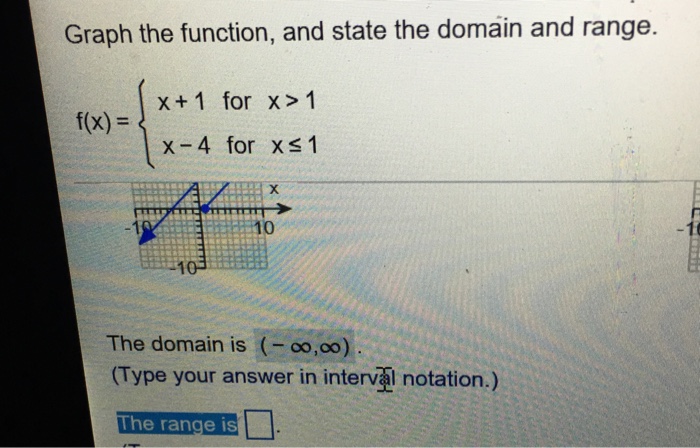



Graph The Function And State The Domain Range F X Chegg Com



Find The Domain And The Range Of The Real Function F Defined By F X Sqrt X 1 Sarthaks Econnect Largest Online Education Community



What Is The Range Of F X X 1 X 1 Quora




Section 1 5 Combinations Of Functions Ppt Download




Domain And Range Calculator Wolfram Alpha




Section 1 1 Relations And Functions Relation Domain Range Function Example 1 State The Domain And Range Of Each Relation Then State Whether Ppt Download
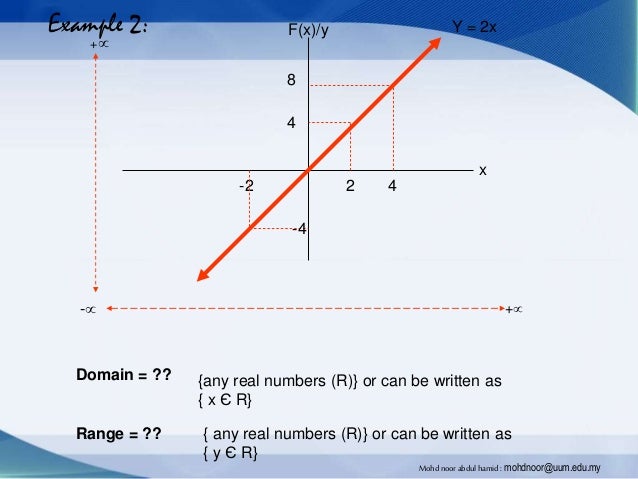



Introduction To Function Domain And Range Mohd Noor




What Are The Domain And Range Of F X 1 6 X 2 Brainly Com



What Is The Range Of The Function F X X 1 Quora




Find The Domain Or Range Of Following Function Tex F X Sqrt X 1 3 X Tex Brainly In




What Are The Domain And Range Of F X 1 5 X Brainly Com
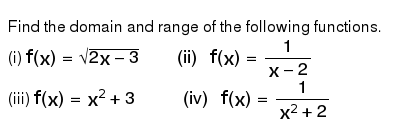



Find The Domain And Range Of The Following Functions I F X Sqrt 2x 3 Ii F X 1 X 2 Iii F X X 2 3 Iv F X 1 X 2 2



Find Domain And Range Of Function Y 1 X 2 Youtube




The Domain Of The Function F X 1 1 E 1x 1 Is



Graph The Function F X Ln X 1 Determine The Domain Range And Vertical Asymptote Enotes Com




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube



Find Domains And Ranges Of The Toolkit Functions College Algebra




Find The Domain And Range Of A Function Learnzillion




Find The Domain And The Range Of The Real Function F X 1 X 3



How Do You Graph F X 2 X 1 3 And State The Domain And Range Socratic




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube



3 3 Domain And Range Mathematics Libretexts




Find The Domain And Range Of Each Of The Following Functions F X X 2 X 1 X 2 4x 3




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In




Example 15 F X 1 X What Is The Domain And Range Examples




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube
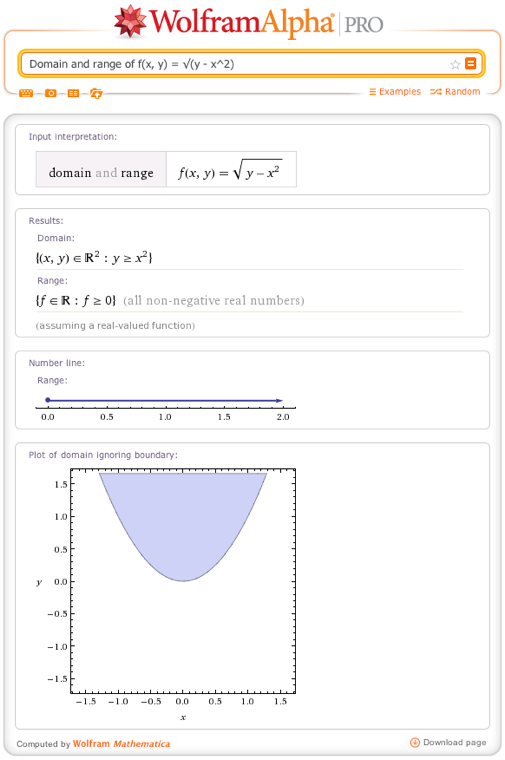



Solve Domain And Range Of A Function With Wolfram Alpha Wolfram Alpha Blog



For The Function F X X 2 5 Find The Domain And Range Enotes Com




Domain And Range Of Quadratic Functions Video Khan Academy



Domain And Range




Find The Domain And Range Of The Function F X 1 Sqrt X 5 Youtube



What Is The Domain And Range Of Y 1 X Quora




View Question What Is The Domain And Range For The Function F X 1 9 X 2




Find The Domain And Range Of F X Root Of X 1 Brainly In




Domain And Range Of 1 X 2 2x 8 Youtube



The Domain And Range Of The Function F X X 2 Is Donimain
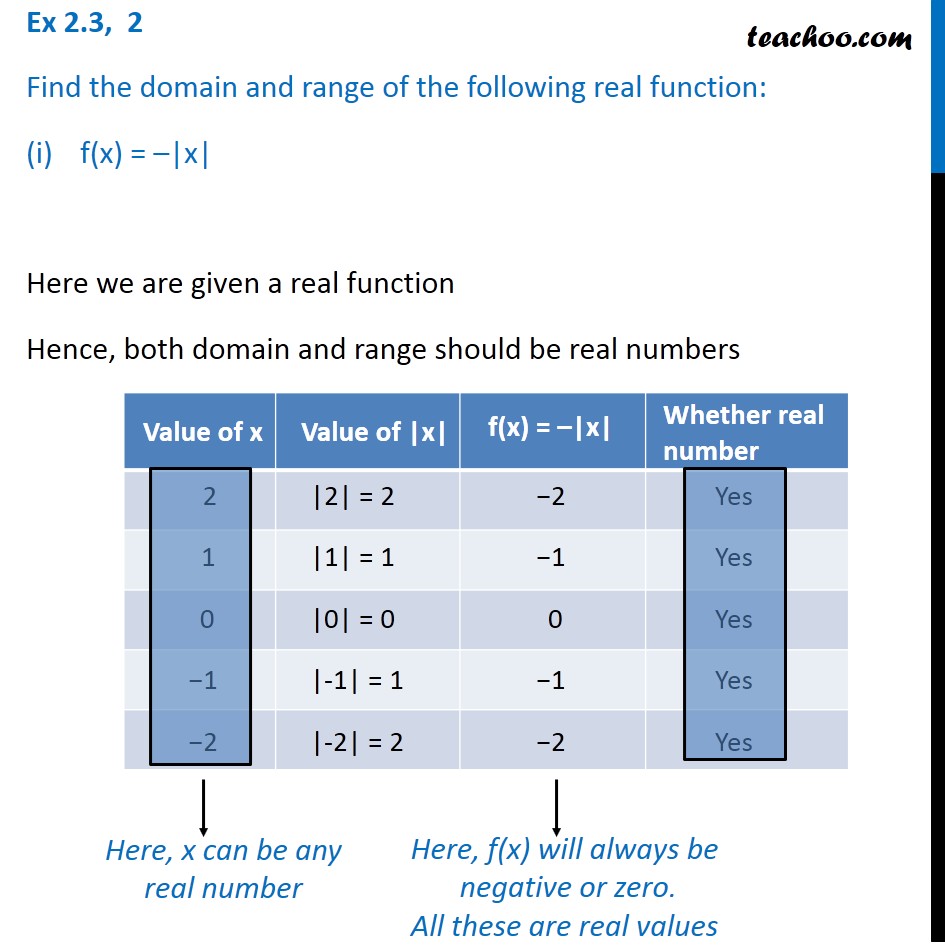



Ex 2 3 2 Find The Domain And Range Of The Function F X X




How To Find Domain And Range Of The Inverse Of A Relation Sat Math



1




Find The Domain And Range Of F X X 1 Youtube




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube
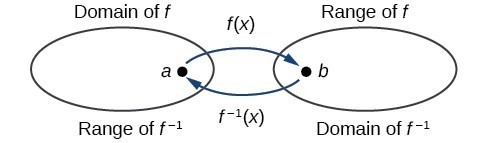



Determine The Domain And Range Of An Inverse Function College Algebra



Domain And Range Of A Function




Example 15 F X 1 X What Is The Domain And Range Examples




A Draw The Graph Of F X X 1 Also Find The Domain And Range Of Maths Relations And Functions Meritnation Com




L1 Functions Domain Amp Range
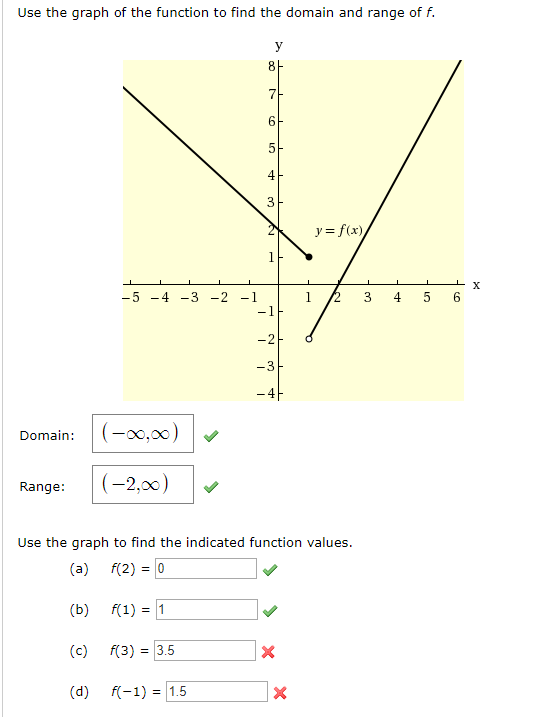



Use The Graph Of The Function To Find The Domain And Chegg Com




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2



Domain And Range Examples Domain And Range Of Functions




How To Find The Domain And Range Of A Function 14 Steps
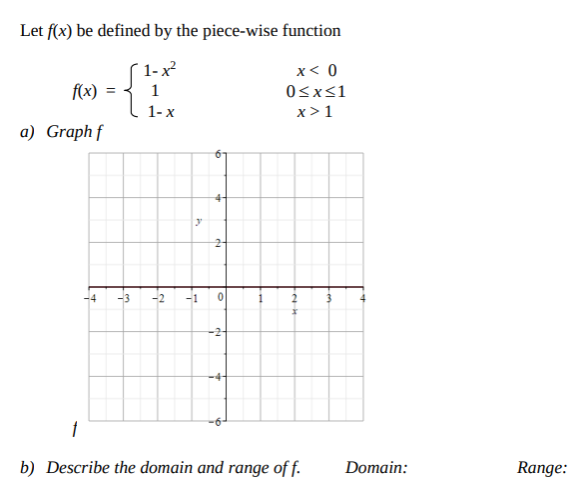



Answered Let F X Be Defined By The Piece Wise Bartleby
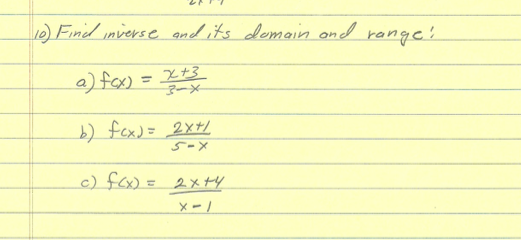



Find Inverse And Its Domain And Range F X X Chegg Com
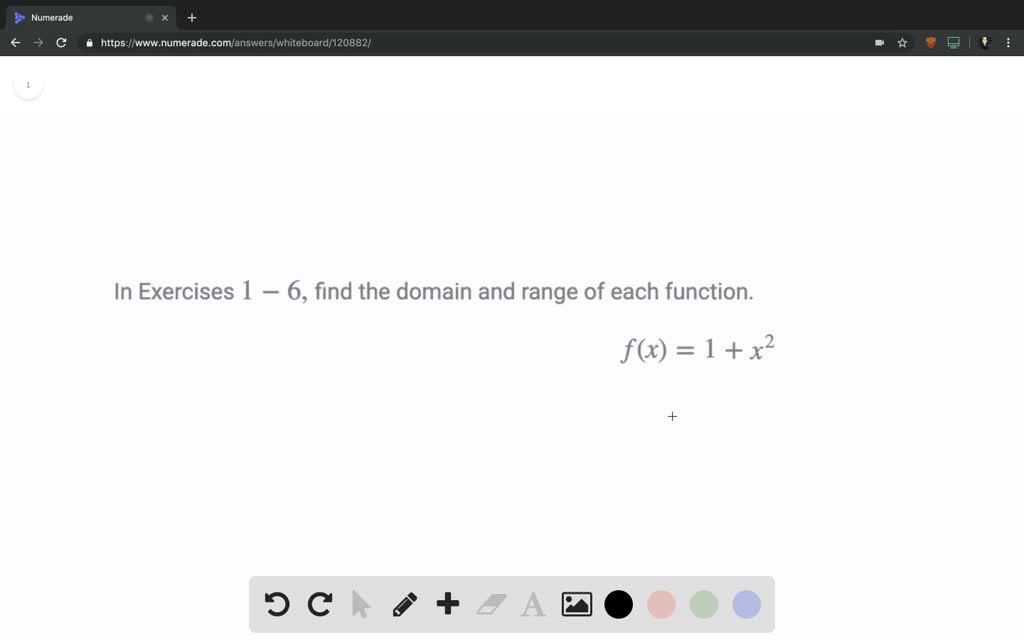



Solved In Exercises 1 6 Find The Domain And Range Of Each Function F X 1 X 2




Domain And Range Of Functions




Domain And Range Free Math Help



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora




Answered In Exercises 1 6 Find The Domain And Bartleby




Example 15 F X 1 X What Is The Domain And Range Examples
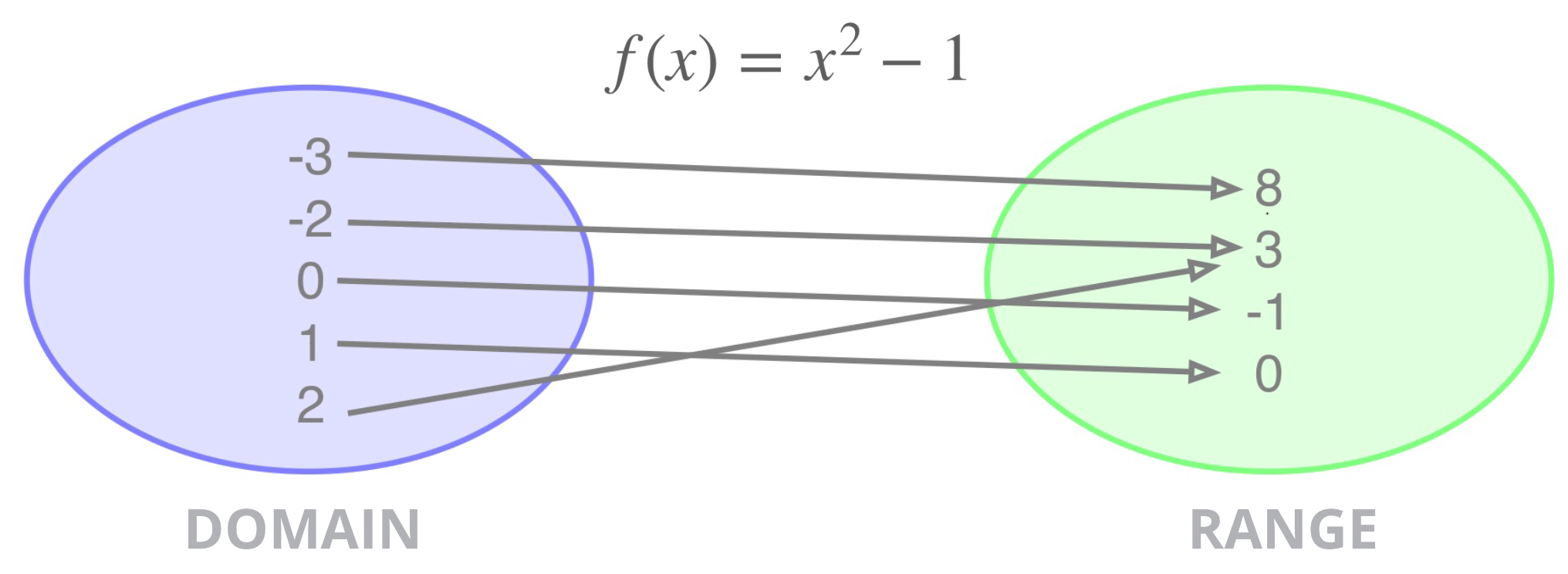



Domain Range A Function




Domain And Range Of F X X 3 X 3 Are Respectively



Domain And Range Of Exponential And Logarithmic Functions
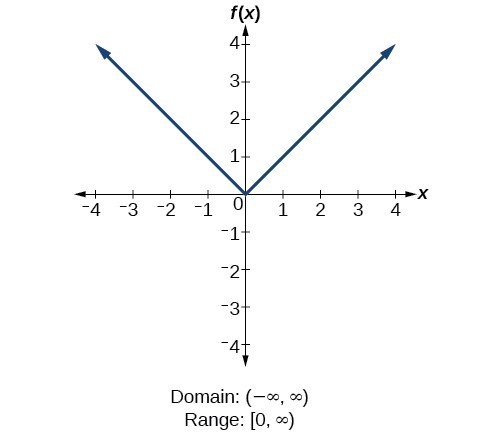



Find Domains And Ranges Of The Toolkit Functions Math 1314 College Algebra




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 3 F X X 1 X 2




Domain And Range Of Quadratic Functions Video Khan Academy




Domain And Range
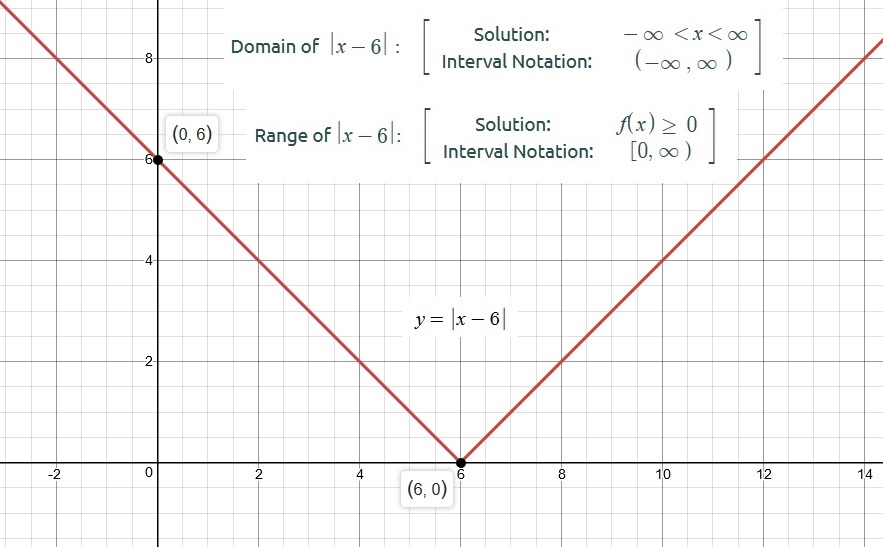



How Do You Find The Domain And Range Of Y X 6 Socratic




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic
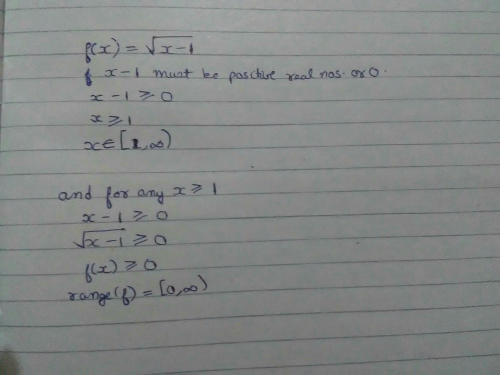



Find The Domain And Range Of Real Function F Defined By F X Underoot Of X 1 Edurev Class 11 Question
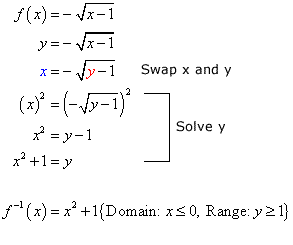



Inverse Of Square Root Function Chilimath




Find The Domain And Range Of The Inverse Of The Given Chegg Com
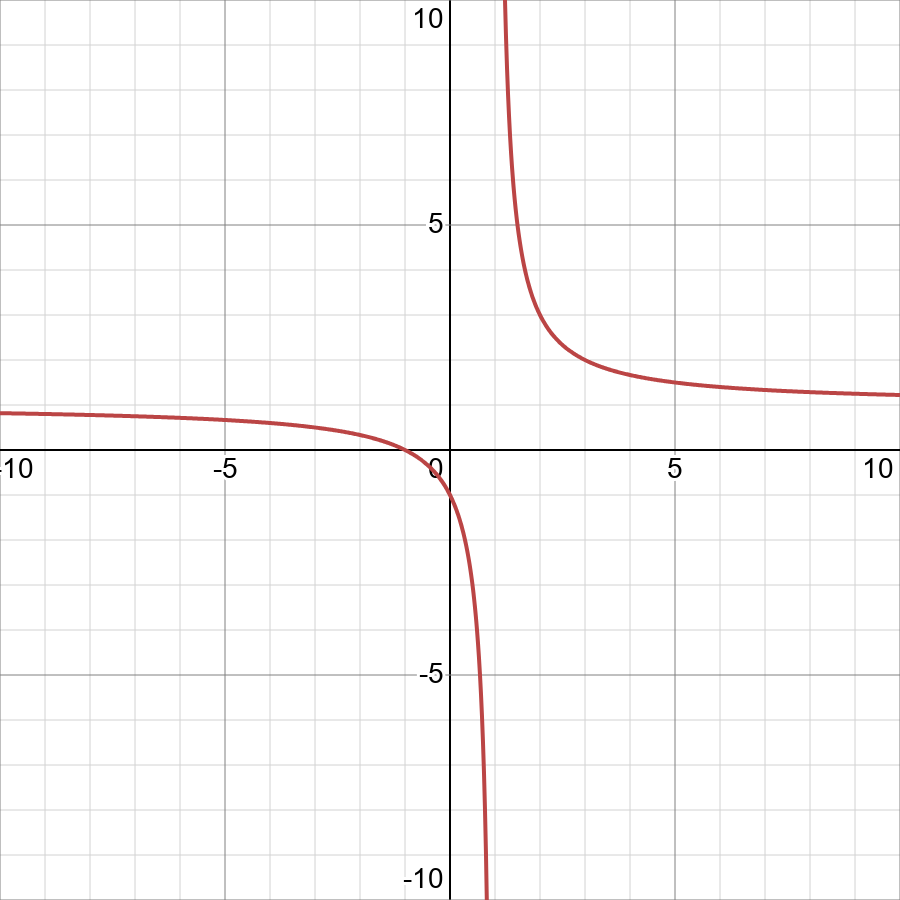



Find The Domain And Range F X X 1 X 1 Displaystyle Fleft Xright Frac X 1 X 1 Snapsolve




Misc 5 Find Domain And Range Of F X X 1 Class 11



0 件のコメント:
コメントを投稿